top of page
f(x)

Building Functions

Read about Building Functions.  Then, test your knowledge!

Click To Watch Your Functions Come To Life!

Building Functions:  Transformations

​

We can move and resize, TRANSFORM, the graphs of functions.

​

Let us start with a function, in this case it is                , but it could be anything:

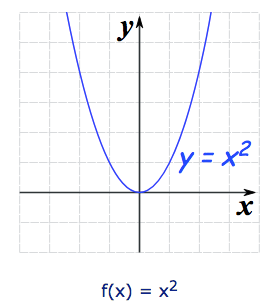
Here are some simple things we can do to move or scale it on the graph:

​

We can move it up or down by adding a constant to the y-value:

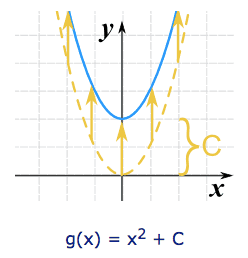
Note: to move the line down, we use a negative value for C.

​

  • C > 0 moves it up

​​

  • C < 0 moves it down

​

We can move it left or right by adding a constant to the x-value:

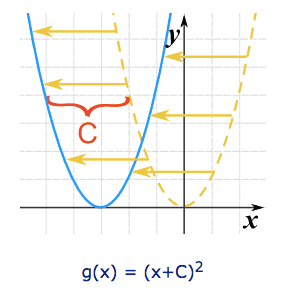
Adding C moves the function to the left (the negative direction).

​

Why? Well imagine you will inherit a fortune when your age=25. If you change that to (age+4) = 25 then you will get it when you are 21. Adding 4 made it happen earlier.

​

  • C > 0 moves it left

​​

  • C < 0 moves it right

 

BUT we must add C wherever x appears in the function (we are substituting x+C for x).

 

Example: the function v(x) = x3 - x2 + 4x

​

To move C spaces to the left, add C to x wherever x appears:

​

w(x) = (x + C)3 − (x + C)2 + 4(x + C)

 

An easy way to remember what happens to the graph when we add a constant:

 

add to y to go high
add to x to go left

 

We can stretch or compress it in the y-direction by multiplying the whole function by a constant.

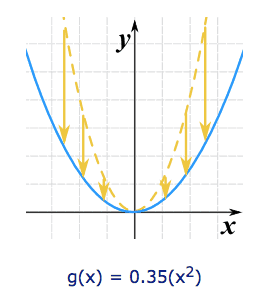
  • C > 1 stretches it

​​

  • 0 < C < 1 compresses it

 

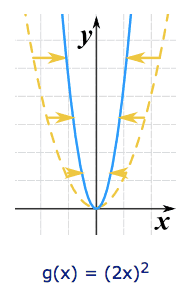
We can stretch or compress it in the x-direction by multiplying x by a constant.

  • C > 1 compresses it

​​

  • 0 < C < 1 stretches it

​​

Note that (unlike for the y-direction), bigger values cause more compression.

 

We can flip it upside down by multiplying the whole function by −1:

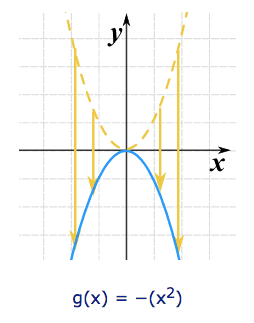
This is also called reflection about the x-axis (the axis where y=0)

​

We can combine a negative value with a scaling:

​

Example: multiplying by −2 will flip it upside down AND stretch it in the y-direction.

 

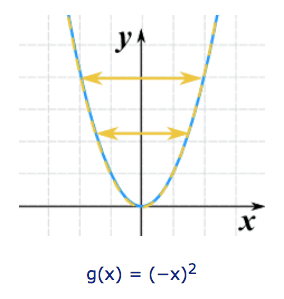
We can flip it left-right by multiplying the x-value by −1:

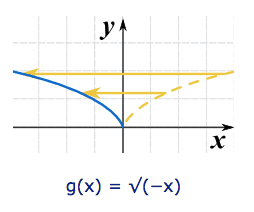
It really does flip it left and right! But you can't see it, because        is symmetrical about the y-axis. So here is another example using √(x):

This is also called reflection about the y-axis (the axis where x=0)

​

​

Summary

This is also called reflection about the y-axis (the axis where x=0)

​

​

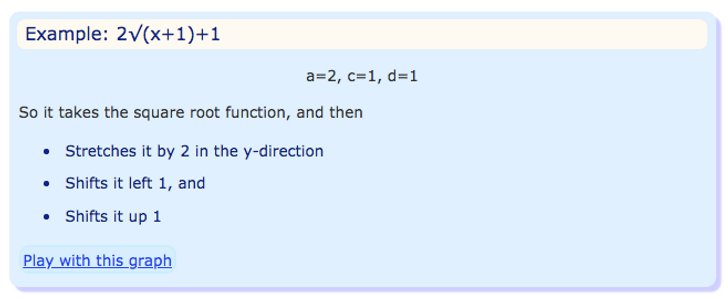
Examples

All In One!

​

We can do all transformation in one go using this:

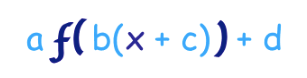
a is vertical stretch/compression

  • |a| > 1 stretches 

  • |a| < 1 compresses 

  • a < 0 flips the graph upside down

 

b is horizontal stretch/compression

  • |b| > 1 compresses 

  • |b| < 1 stretches 

  • b < 0 flips the graph left-right

 

c is horizontal shift

  • c < 0 shifts to the right 

  • c > 0 shifts to the left

 

d is vertical shift

  • d > 0 shifts upward 

  • d < 0 shifts downward

bottom of page