Benjamin Franklin K-8 Center, Algebra I E.O.C.
Algebra & Math Education
Rewriting
rational expressions
Watch and complete your notes on the videos below.
Afterwards, read about Rewriting Rational Expressions. Then, test your knowledge!
Multiplying Polynomials
​
To multiply two polynomials:
​
-
multiply each term in one polynomial by each term in the other polynomial
​​
-
add those answers together, and simplify if needed
​​
Let us look at the simplest cases first.
​
1 term × 1 term (monomial times monomial)
​
To multiply one term by another term, first multiply the constants, then multiply each variable together and combine the result, like this (press play):
​
​
​
​
​
​
​
​
(Note: I used "·" to mean multiply. In Algebra we don't like to use "×" because it looks too much like the letter "x")
​
1 term × 2 terms (monomial times binomial)
​
Multiply the single term by each of the two terms, like this:
​
​
​
​
​
​
​
2 term × 1 terms (binomial times monomial)
​
Multiply each of the two terms by the single term, like this:
​
​
​
​
​
​
​
​
​
​
​
​
​
(That was a bit faster because you can use mental math before writing it down.)
​
2 terms × 2 terms (binomial times binomial)
​
Each of the two terms in the first binomial ...
... is multiplied by ...
... each of the two terms in the second binomial
​
​
That is 4 different multiplications ... Why?
It is the same when we multiply binomials!
​
Instead of Alice and Betty, let's just use a and b, and Charles and David can be c and d:
​
​
We can multiply them in any order so long as each of the first two terms gets multiplied by each of the second two terms.
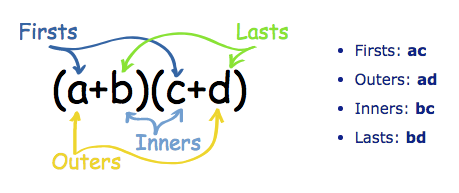
But there is a handy way to help us remember to multiply each term called "FOIL".
​
It stands for "Firsts, Outers, Inners, Lasts":
​
​
​
​
​
​
​
​
​
​
​
So you multiply the "Firsts" (the first terms of both polynomials), then the "Outers", etc.
​
Let us try this on a more complicated example:
​
​
​
​
​
​
​
​
​
​
​
​
​
2 terms × 3 terms (binomial times trinomial)
​
"FOIL" won't work here, because there are more terms now. But just remember:
​
Multiply each term in the first polynomial by each term in the second polynomial.
​
​
​
​
​
​
​
​
​
​
​
​
​
​
​
​
​
​
Like Terms
​
And always remember to add Like Terms:
